Truncated triheptagonal tiling
| Truncated triheptagonal tiling | |
|---|---|
Poincaré_disk_model |
|
| Type | Hyperbolic semiregular tiling |
| Vertex figure | 4.6.14 |
| Schläfli symbol | 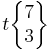 or t0,1,2{7,3} or t0,1,2{7,3} |
| Wythoff symbol | 2 7 3 | |
| Coxeter-Dynkin | |
| Symmetry | [7,3] |
| Dual | Order-3 bisected heptagonal tiling |
| Properties | Vertex-transitive |
In geometry, the truncated triheptagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one hexagon, and one tetrakaidecagon (14-sides) on each vertex. It has Schläfli symbol of t0,1,2{7,3}.
Contents |
Iniform colorings
There is only one uniform colorings of a truncated triheptagonal tiling. (Naming the colors by indices around a vertex: 123.)
Related polyhedra and tilings
This tiling is topologically related as a part of sequence of omnitruncated polyhedra with vertex figure (4.6.2n). This set of polyhedra are zonohedrons.
(4.6.4) |
(4.6.6) |
(4.6.8) |
(4.6.10) |
(4.6.12) |
(4.6.14) |
(4.6.16) |
(4.6.∞) |
Dual tiling
The dual tiling is called an order-3 bisected heptagonal tiling, made as a complete bisection of the order-3 heptagonal tiling, here with triangles colored alternatingly white and blue.
Each triangle in this dual tiling represent a fundamental domain of the Wythoff construction for the symmetry group [7,3].
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, LCCN 99-35678, ISBN 0-486-40919-8 (Chapter 10: Regular honeycombs in hyperbolic space)